By OCAdmin in Research highlights on

Yong-Jin Huang, Chun-Wei Chang, and Chih-hao Hsieh

A long-standing central challenge in natural science is to detect the change point (aka regime shift) in the dynamics of natural systems using historical data. To address this scientific problem, a novel method, Nested-Library Analysis, is developed by the master graduate Yong-Jin Huang and Prof. Chih-hao Hsieh from the Institute of Oceanography and Prof. Chun-Wei Chang from the Institute of Fisheries Science, NTU. This new method can be applied to all kinds of natural systems and well estimates the change point even under the condition where the abrupt change in the underlying mechanism is not reflected by the statistical distribution of the data segment. This work is published in PLOS Computational Biology in Jan. 2024.

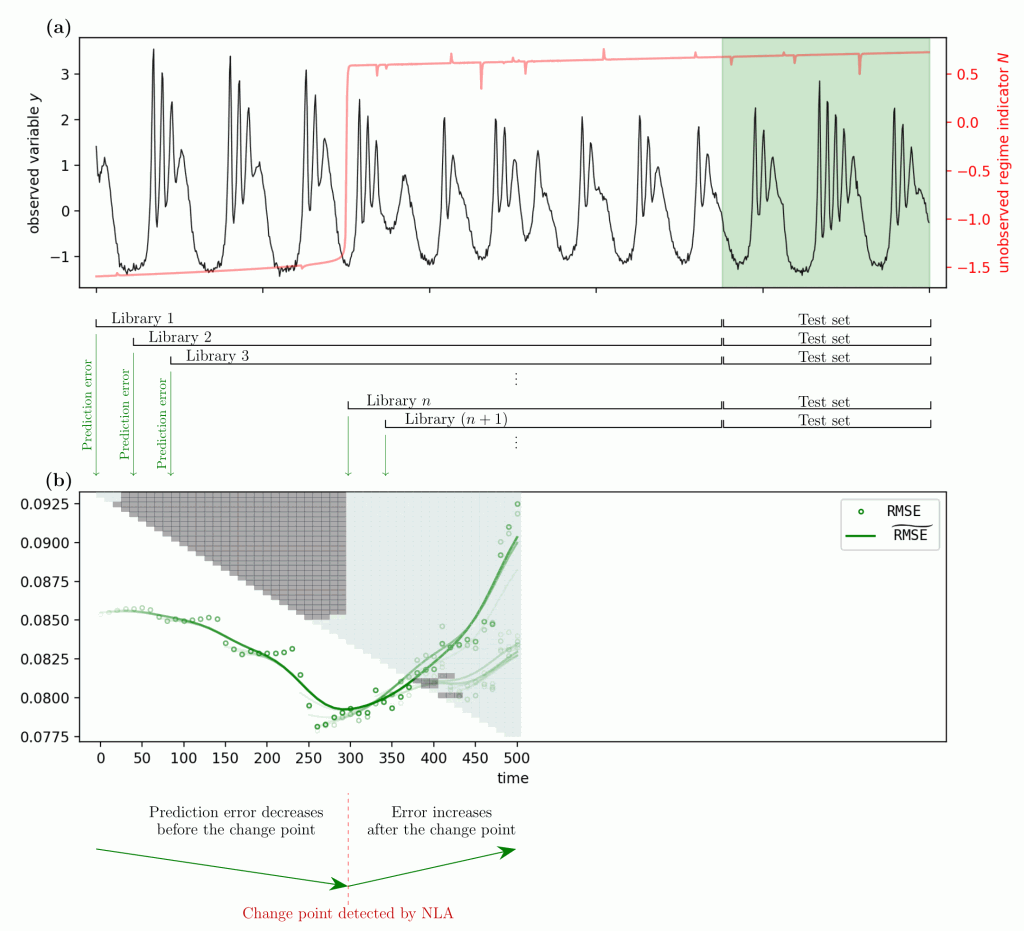
A natural system of interest is rarely described as a closed system; therefore, the system may have undergone a regime shift. Such a shift could result from a sudden fluctuation caused by external force, or a critical transition taking place when certain gradually changing parameter reaches a critical threshold. These regime-shift events can exert a great influence on the dynamics of a system. However, the “significant change” may be difficult to identify, because (i) nonlinearity or even chaos present in the system dynamics, (ii) system variables that exhibit apparent shifts may be unobserved, and (iii) low signal-to-noise ratio occurs in the data. In fact, these problematic conditions are ubiquitous; however, existing change-point detection methods did not take the former two issues into consideration. In this research, by sequentially eliminating historical data points in the library/training set to optimize the performance of Empirical Dynamic Modeling (EDM), Nested-Library Analysis serves as a generic automatic detection method (Figure 1). Investigations using model data indicate that NLA overcomes the limitations and outperforms all existing detection methods. As a real-world example, NLA successfully detects the change point in the Pacific Decadal Oscillation index, which is highly consistent with the change point reported in the literature.

This novel and generic detection algorithm provides an effective tool for natural sciences and environmental managements. By applying NLA as an ad hoc analysis, one can identify several periods from time series data that are supposed to be modeled separately, so as to ensure the validity of argument in analysis and improve the forecast ability. Otherwise, overlooking or wrongly estimating of occurrence of dynamical shifts could result in inappropriate employment of a forecast model or analysis. Moreover, the NLA method can even be used to reveal the abrupt shifts in system that, otherwise, was unnoticed by looking at the statistical properties of time series data per se; thus, NLA provides insights into further investigation on the underlying mechanism as well as its cause and consequence.

Figure 1. Schematic illustrating Nested-Library Analysis (NLA) to detect abrupt shifts in dynamics. In (a), the black line represents the observation data of a species y in a chaotic ecological system, while the red line illustrates a latent variable N (assumed to be unobserved/unobservable). In this example, the latent variable determines the interaction strength between the species x and y. However, there is no significant change in the data distribution of the species y, a situation where existing detection methods fail. In NLA, we sequentially eliminate data points from the library set (the part of observation data without green background), quantifying the performance of EDM using prediction error. Then, the result is obtained as (b). Since the performance of EDM is optimized when it just excludes all the data points of which underlying mechanism is distinct from that of test set (with green background in (a)), we can conclude whether and when an abrupt shift occurs in the system according to the change in the error curve.

Reference

Huang, Y. J., Chang, C. W., & Hsieh, C. H. (2024). Detecting shifts in nonlinear dynamics using Empirical Dynamic Modeling with Nested-Library Analysis. PLOS Computational Biology, 20(1), e1011759.